Rentesregning Excel

Excel-funktioner til finansielle beregninger

Excel tilbyder en række funktioner til finansielle beregninger, disse funktioner gennemgås på denne side med eksempler og forklaringer.
Disse funktioner kan anvendes både til annuiteter (se særskilt kapitel) og til enkeltstående kapitalbeløb:

Funktion	Engelsk Funktion	Beskrivelse	Forklaring
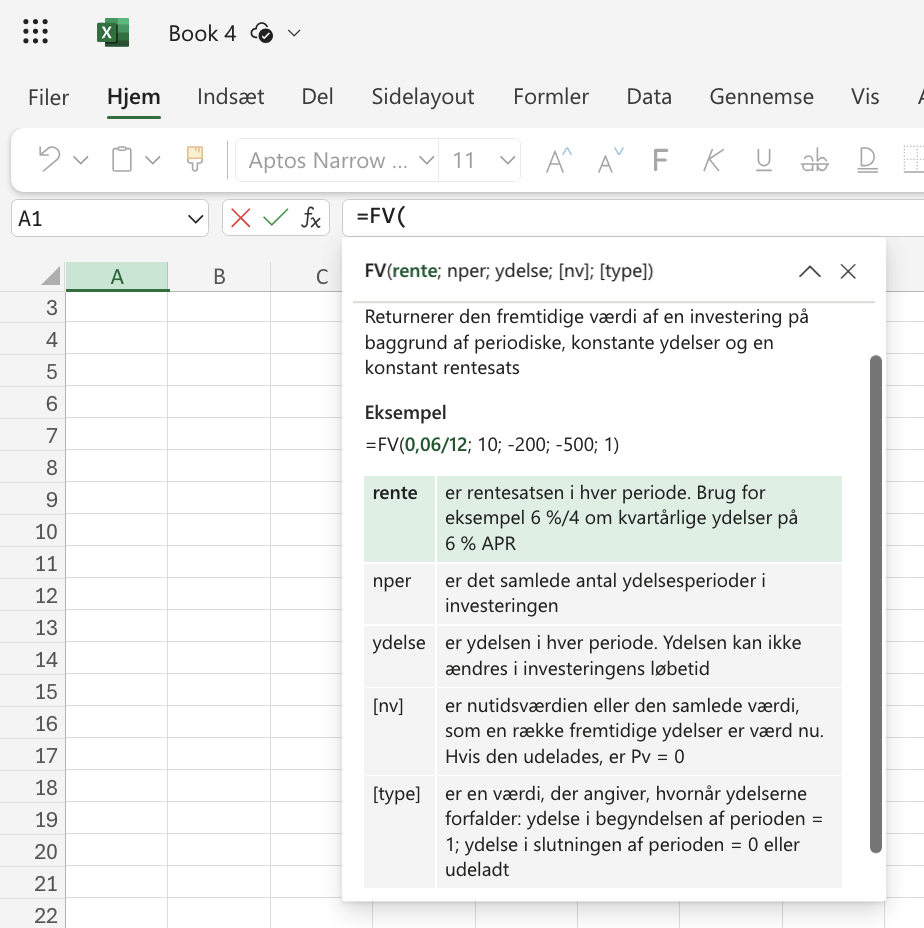
FV	FV	(Fremtidsværdi)	Beregner den fremtidige værdi af en investering baseret på periodiske, konstante betalinger og en konstant rente. Kan også bruges til at beregne fremtidsværdien af en enkeltstående kapital ved at sætte Ydelse til 0 eller lade den være tom.
NPER	NPER	Antal perioder	Beregner antallet af perioder for en investering baseret på periodiske, konstante betalinger og en konstant rente. Kan også bruges til at beregne, hvor lang tid det tager for en kapital at vokse til et bestemt beløb ved at sætte Ydelse til 0 eller lade den være tom.
NV	PV	Nutidsværdi	Beregner den nuværende værdi af en investering baseret på fremtidige betalinger. Kan også bruges til at beregne nutidsværdien af et fremtidigt enkeltstående beløb ved at sætte Ydelse til 0 eller lade den være tom.
RENTE	RATE	Terminsrenten	Beregner rentesatsen pr. periode for en annuitet. Kan også bruges til at beregne vækstraten for en kapital over en given periode ved at sætte Ydelse til 0 eller lade den være tom.
YDELSE	PMT	Ydelsen pr. termin	Beregner betalingen for et lån baseret på konstante betalinger og en konstant rente (disse lige store betalinger kaldes for en annuitet). Kan også bruges til at beregne den nødvendige periodiske indbetaling for at nå et opsparingsmål.

Det er værd at bemærke, at disse funktioner kan bruges til rentesregning ved at sætte Ydelse til 0 eller lade den være tom. Dette er nyttigt, når man arbejder med enkeltstående ind- eller udbetalinger frem for regelmæssige betalinger.
En vigtig detalje at huske er, at alle disse finansfunktioner indeholder et argument kaldet "type". Dette argument angiver, om betalinger foretages i begyndelsen eller slutningen af hver periode. Normalt sætter vi ikke noget ind i dette argument, da ydelser typisk betales sidst i terminen. Excel antager som standard, at betalinger sker i slutningen af perioden, hvis type-argumentet udelades.

Ved at justere de forskellige parametre i disse funktioner, kan man løse mange finansielle opgaver, fra simple renteberegninger til mere komplekse investeringsanalyser.

Fremskrivning af kapital

Fremskrivning af kapital er en grundlæggende økonomisk beregning, der viser, hvordan penge vokser over tid.
Fremskrivning tager højde for rentes rente effekten, hvilket betyder, at man ikke bare tjener renter på den oprindelige investering, men også på de renter, der er optjent i tidligere perioder.

Eksempel FV 1:

Tekst	Værdier	Excel uden FV	Excel med FV	Resultat
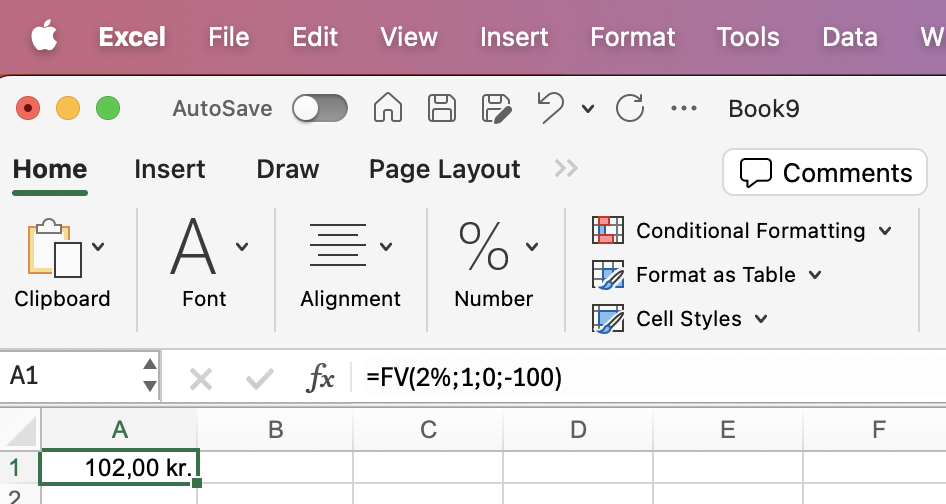
En opsparing på 100 kr. vokser med en årlig rente på 2% over 1 år	Startkapital = 100 Rente = 2% År = 1	=100*(1+2%)^1	=FV(2%;1;0;-100)	102,00 kr.

Eksempel FV 2:

Tekst	Værdier	Excel uden FV	Excel med FV	Resultat
En opsparing på 100 kr. vokser med en årlig rente på 2% over 2 år	Startkapital = 100 Rente = 2% År = 1	=100*(1+2%)^1	=FV(2%;1;0;-100)	104,40 kr.

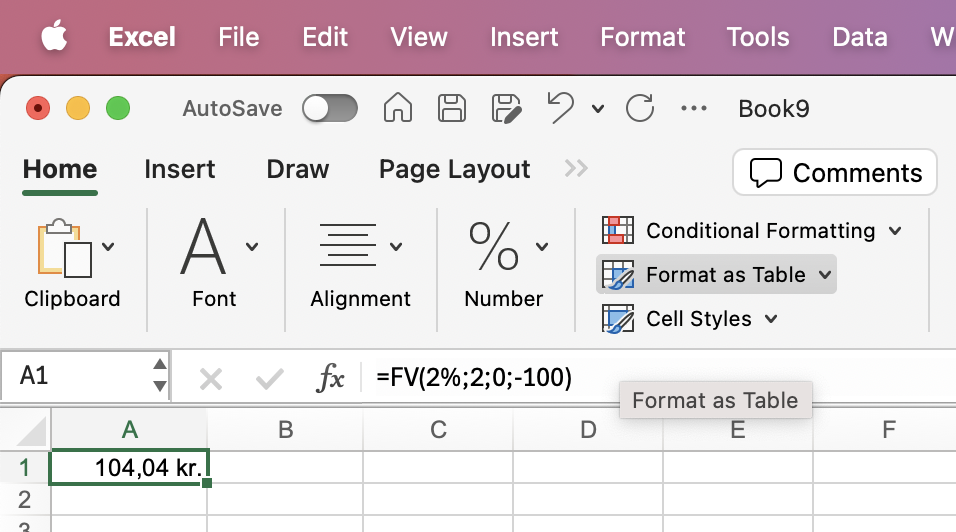Bemærk på grund af renters rente vokser kapitalen til 104,40 kr. og ikke blot 104,00 kr.

Eksempel FV 3:

Tekst	Værdier	Excel uden FV	Excel med FV	Resultat
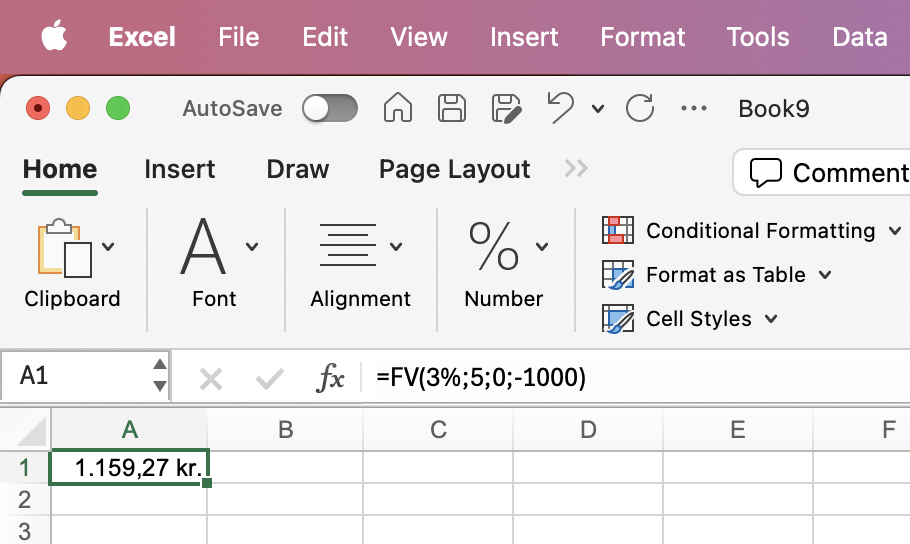
En opsparing på 1000 kr. vokser med en årlig rente på 3% over 5 år	Startkapital = 1000 Rente = 3% År = 5	=1000*(1+3%)^5	=FV(3%;5;0;-1000)	1159,27 kr.

Eksempel FV 4:

Tekst	Værdier	Excel uden FV	Excel med FV	Resultat
En opsparing på 10000 kr. vokser med en årlig rente på 4% over 20 år	Startkapital = 10000 Rente = 4% År = 20	=10000*(1+4%)^20	=FV(4%;20;0;-10000)	21911,23 kr.

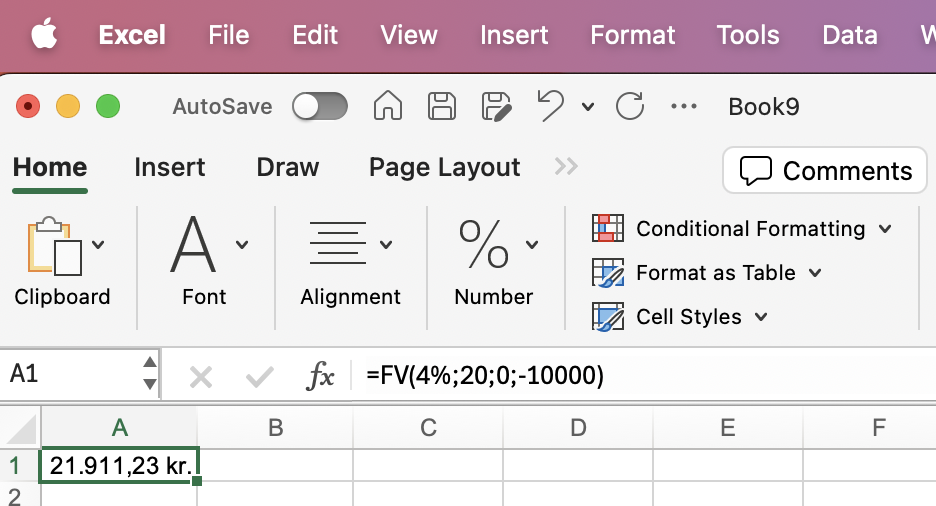Disse eksempler illustrerer, hvordan en kapital vokser over forskellige tidshorisonter. Bemærk, at jo længere tidshorisonten er, desto større bliver effekten af rentes rente. Excel's FV-funktion gør beregningerne enklere, men det er også muligt at udføre beregningerne uden denne funktion ved at bruge formlen for renters rente:
Slutværdi = Startkapital * (1 + rente)^år.

Nutidsværdi af kapital

Nutidsværdi er en fundamental økonomisk beregning, der viser værdien af fremtidige pengestrømme omregnet til nutidens værdi. Dette koncept er vigtigt for at forstå, hvordan fremtidige beløb skal vurderes i dag, givet at penge har en tidsværdi. Nutidsværdiberegninger tager højde for, at et beløb modtaget i fremtiden er mindre værd end det samme beløb modtaget i dag, primært på grund af inflation og alternative investeringsmuligheder.

Eksempel NV 1:

Tekst	Værdier	Excel uden NV	Excel med NV	Resultat
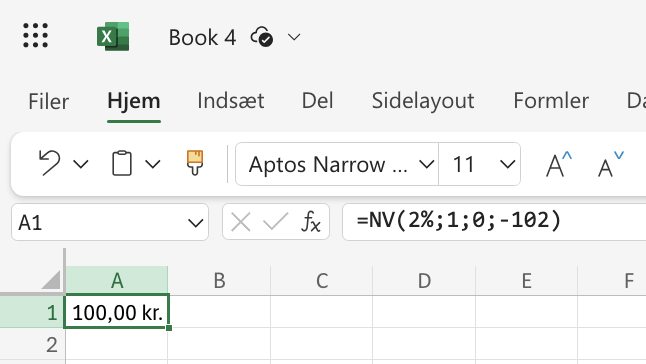
Nutidsværdien af 102 kr. om 1 år med en diskonteringsrente på 2%	Fremtidigt beløb = 102 Rente = 2% År = 1	=102/(1+2%)^1	=NV(2%;1;0;-102)	100,00 kr.

Eksempel NV 2:

Tekst	Værdier	Excel uden NV	Excel med NV	Resultat
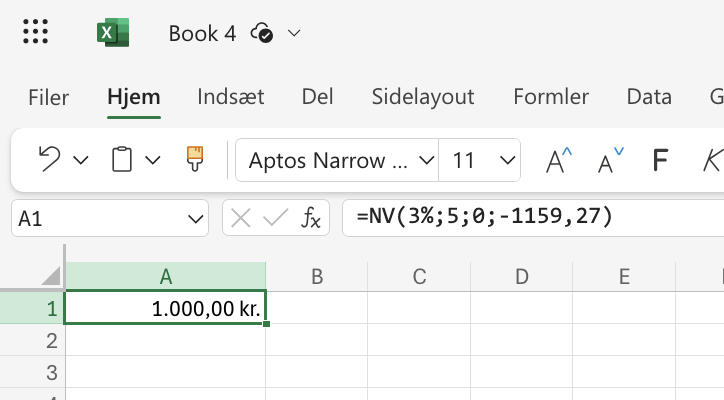
Nutidsværdien af 1159,27 kr. om 5 år med en diskonteringsrente på 3%	Fremtidigt beløb = 1159,27 Rente = 3% År = 5	=1159,27/(1+3%)^5	=NV(3%;5;0;-1159,27)	1000,00 kr.

Eksempel NV 3:

Tekst	Værdier	Excel uden NV	Excel med NV	Resultat
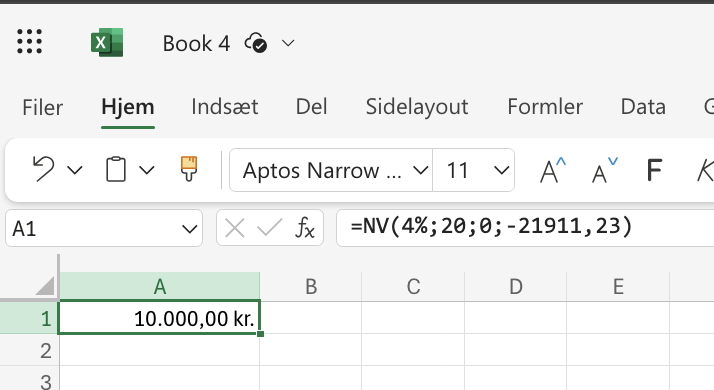
Nutidsværdien af 21911,23 kr. om 20 år med en diskonteringsrente på 4%	Fremtidigt beløb = 21911,23 Rente = 4% År = 20	=21911,23/(1+4%)^20	=NV(4%;20;0;-21911,23)	10000,00 kr.

Disse eksempler illustrerer, hvordan nutidsværdien af et fremtidigt beløb beregnes over forskellige tidshorisonter. Bemærk, at jo længere tidshorisonten er, desto mindre bliver nutidsværdien af et givet fremtidigt beløb. Excel's NV-funktion gør beregningerne enklere, men det er også muligt at udføre beregningerne uden denne funktion ved at bruge formlen for nutidsværdi: Nutidsværdi = Fremtidigt beløb / (1 + rente)^år.

Beregning af antal perioder for kapitalvækst

Når man investerer kapital eller optager et lån, er det ofte relevant at vide, hvor lang tid det tager før kapitalen er vokset til et bestemt beløb. Dette kan beregnes ved hjælp af renters rente-formlen og logaritmer. Excel tilbyder også en funktion, NPER, der gør beregningen enkel.

Eksempel NPER 1:

Tekst	Værdier	Excel uden NPER	Excel med NPER	Resultat
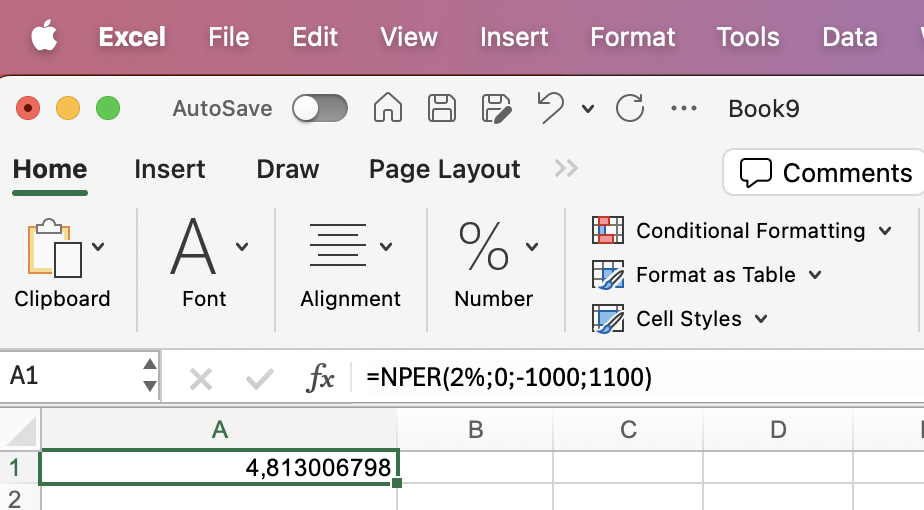
Hvor mange år tager det for 1000 kr. at vokse til 1100 kr. med en rente på 2% p.a.?	Startkapital = 1000 Slutkapital = 1100 Rente = 2%	=LN(1100/1000)/LN(1+2%)	=NPER(2%;0;-1000;1100)	4,81 år

Eksempel NPER 2:

Tekst	Værdier	Excel uden NPER	Excel med NPER	Resultat
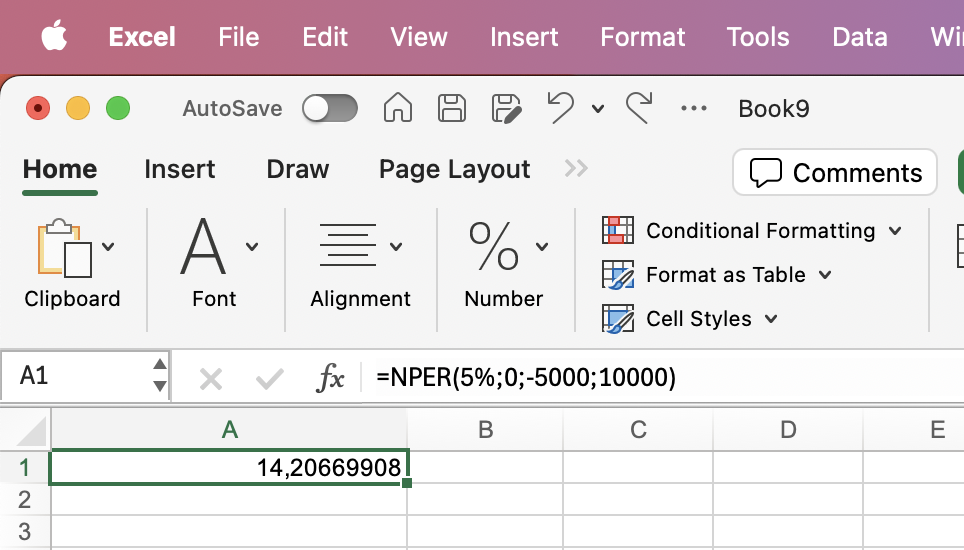
Hvor mange år tager det for 5000 kr. at fordobles med en rente på 5% p.a.?	Startkapital = 5000 Slutkapital = 10000 Rente = 5%	=LN(10000/5000)/LN(1+5%)	=NPER(5%;0;-5000;10000)	14,21 år

Eksempel NPER 3:

Tekst	Værdier	Excel uden NPER	Excel med NPER	Resultat
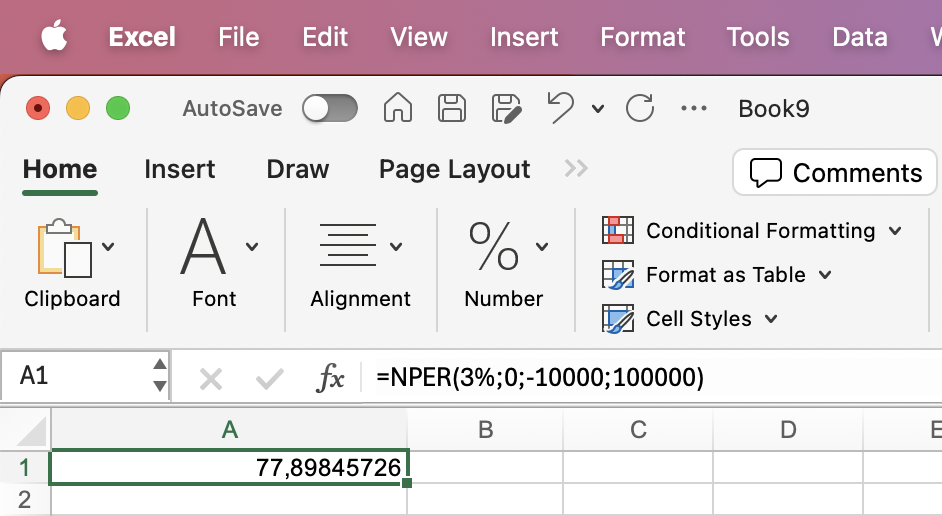
Hvor mange år tager det for 10000 kr. at vokse til 100000 kr. med en rente på 3% p.a.?	Startkapital = 10000 Slutkapital = 100000 Rente = 3%	=LN(100000/10000)/LN(1+3%)	=NPER(3%;0;-10000;100000)	77,90 år

Disse eksempler viser, hvordan man kan beregne det antal perioder (år), det tager for en given startkapital at vokse til en ønsket slutkapital ved en bestemt rente. Formlen uden brug af Excel's NPER-funktion er baseret på logaritmer: Antal perioder = LN(Slutkapital/Startkapital) / LN(1+rente). Excel's NPER-funktion gør beregningen enklere, men det er nyttigt at forstå den underliggende formel. Bemærk, at jo lavere renten er, eller jo større forskellen er mellem start- og slutkapital, desto længere tid tager det for kapitalen at vokse til det ønskede beløb.

Beregning af rente

At beregne renten er en vigtig del af mange finansielle analyser. Hvad enten det drejer sig om investeringer, lån eller opsparinger, er det ofte nødvendigt at finde den effektive rente. Excel's RENTE-funktion gør denne beregning enkel, men det er også muligt at udføre beregningen manuelt.

Eksempel RENTE 1:

Tekst	Værdier	Excel uden RENTE	Excel med RENTE	Resultat
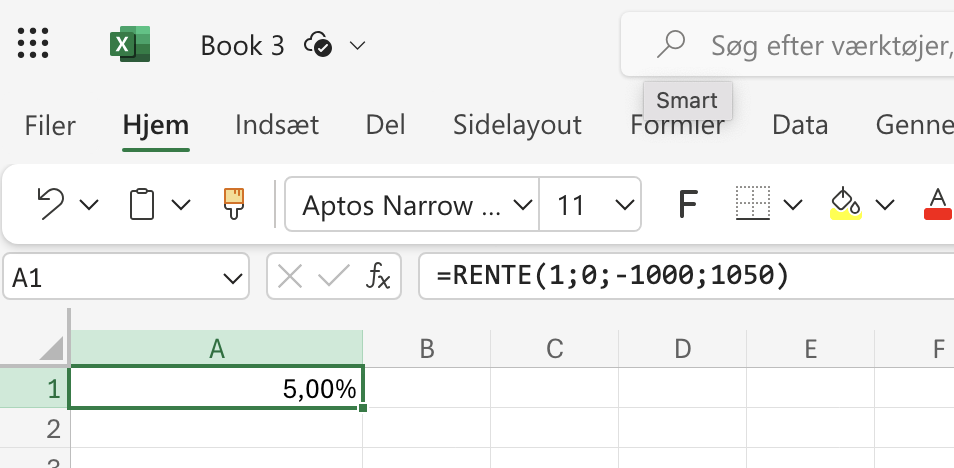
Hvad er den årlige rente, hvis 1000 kr. vokser til 1050 kr. på 1 år?	Startkapital = 1000 Slutkapital = 1050 År = 1	=(1050/1000)^(1/1)-1	=RENTE(1;0;-1000;1050)	5,00%

Eksempel RENTE 2:

Tekst	Værdier	Excel uden RENTE	Excel med RENTE	Resultat
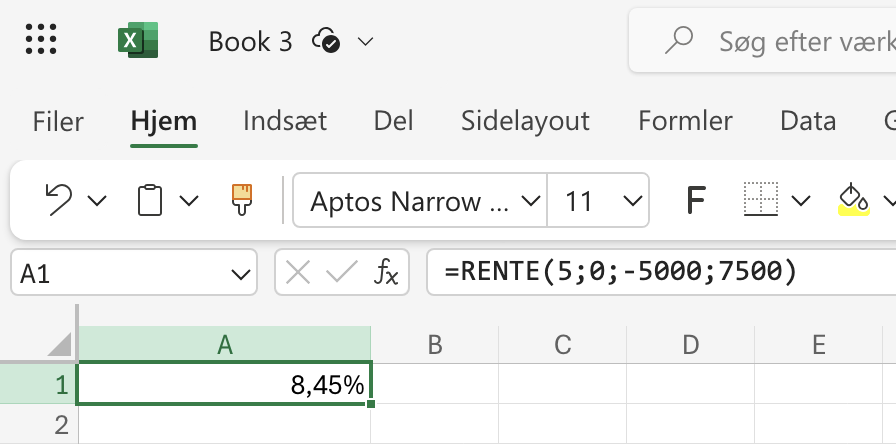
Hvad er den årlige rente, hvis 5000 kr. vokser til 7500 kr. på 5 år?	Startkapital = 5000 Slutkapital = 7500 År = 5	=(7500/5000)^(1/5)-1	=RENTE(5;0;-5000;7500)	8,45%

Eksempel RENTE 3:

Tekst	Værdier	Excel uden RENTE	Excel med RENTE	Resultat
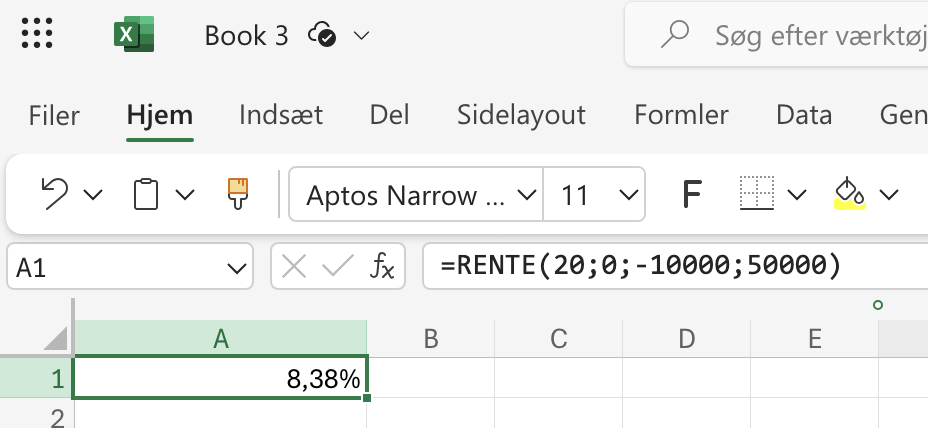
Hvad er den årlige rente, hvis 10000 kr. vokser til 50000 kr. på 20 år?	Startkapital = 10000 Slutkapital = 50000 År = 20	=(50000/10000)^(1/20)-1	=RENTE(20;0;-10000;50000)	8,38%

Disse eksempler illustrerer, hvordan man kan beregne den årlige rente for forskellige scenarier ved hjælp af Excel's RENTE-funktion. Formlen uden brug af RENTE-funktionen er baseret på n'te rod: Årlig rente = (Slutkapital/Startkapital)^(1/antal år) - 1. Excel's RENTE-funktion gør beregningen enklere, men det er nyttigt at forstå den underliggende formel. Bemærk, at jo kortere perioden er, eller jo større forskellen er mellem start- og slutkapital, desto højere bliver den beregnede rente.

Beregning af årlig effektiv rente fra terminsrente

Når man arbejder med investeringer eller lån, støder man ofte på renter opgivet for forskellige terminer. For at sammenligne disse renter korrekt, er det nødvendigt at omregne dem til en fælles basis, typisk den årlige effektive rente.

Det er vigtigt at være opmærksom på, at den terminsrente, som banker ofte viser i deres dokumenter, typisk er omregnet til en årlig nominel rente. Denne årlige nominelle rente er lavere end den reelle årlige effektive rente. For eksempel kan en bank angive en månedlig rente på 0,5%, hvilket giver en årlig nominel rente på:
6% (0,5% * 12 måneder)
Men den årlige effektive rente, som tager højde for renters rente, vil være højere, nemlig:
6,17% ((1 + 0,5%)^12 - 1)
Denne forskel kan virke lille, men over tid og ved større beløb kan den have en betydelig indvirkning på de samlede omkostninger eller afkast.

Eksempel 1: Månedlig til årlig rente

Tekst	Værdier	Excel-formel	Resultat
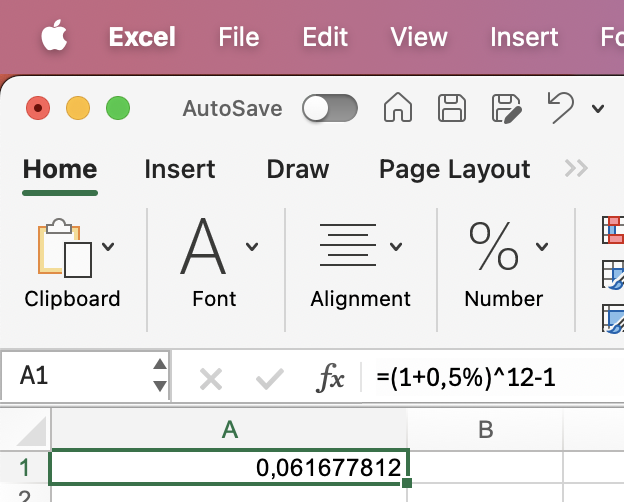
Hvad er den årlige effektive rente, hvis den månedlige rente er 0,5%?	Månedlig rente = 0,5% Terminer pr. år = 12	=(1+0,5%)^12-1	6,17%

Eksempel 2: Kvartalsvis til årlig rente

Tekst	Værdier	Excel-formel	Resultat
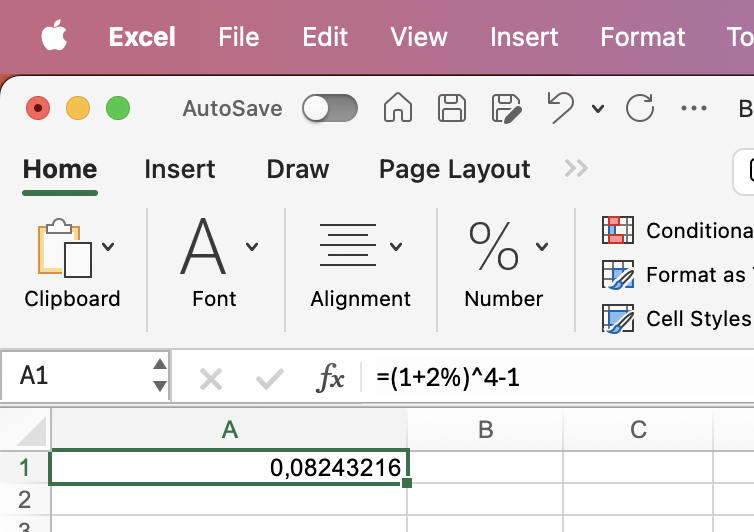
Hvad er den årlige effektive rente, hvis den kvartalsvise rente er 2%?	Kvartalsvis rente = 2% Terminer pr. år = 4	=(1+2%)^4-1	8,24%

Eksempel 3: Daglig til årlig rente

Tekst	Værdier	Excel-formel	Resultat
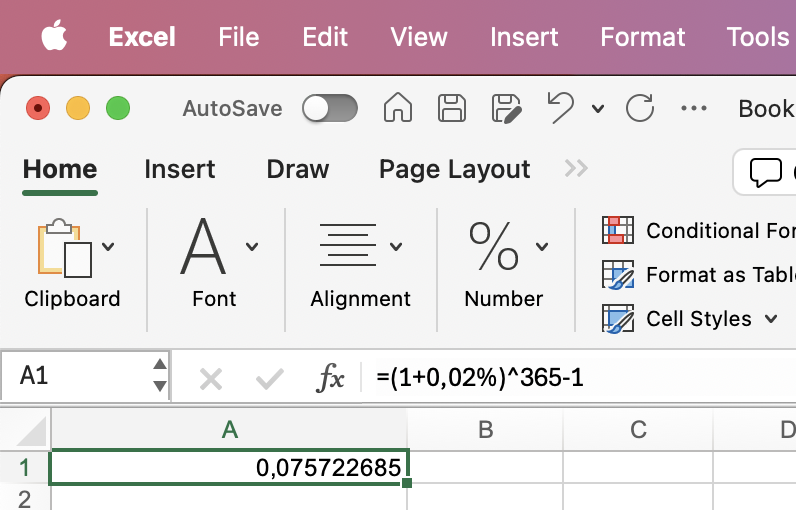
Hvad er den årlige effektive rente, hvis den daglige rente er 0,02%?	Daglig rente = 0,02% Terminer pr. år = 365	=(1+0,02%)^365-1	7,57%

Disse eksempler viser, hvordan man kan beregne den årlige effektive rente ud fra terminsrenter. Formlen er: Årlig effektiv rente = (1 + terminsrente)^(antal terminer pr. år) - 1. Bemærk, at den årlige effektive rente altid vil være højere end den nominelle årlige rente (terminsrente * antal terminer) på grund af renters rente effekten. Jo flere terminer pr. år, desto større bliver forskellen mellem den nominelle og den effektive rente.

Beregning af terminsrente fra årlig effektiv rente

I mange finansielle situationer er det nødvendigt at omregne en årlig effektiv rente til en terminsrente, for eksempel for at beregne månedlige ydelser på et lån. Denne omregning tager højde for renters rente effekten og sikrer præcise beregninger.

Eksempel 1: Årlig til månedlig rente

Tekst	Værdier	Excel-formel	Resultat
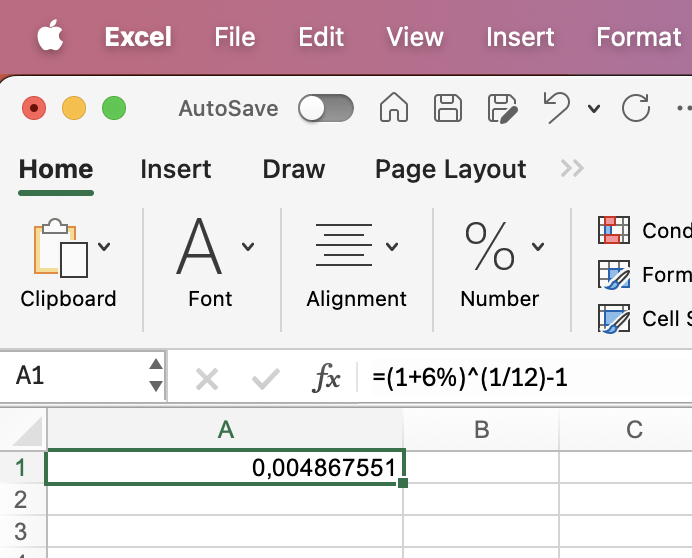
Hvad er den månedlige rente, hvis den årlige effektive rente er 6%?	Årlig effektiv rente = 6% Terminer pr. år = 12	=(1+6%)^(1/12)-1	0,49%

Eksempel 2: Årlig til kvartalsvis rente

Tekst	Værdier	Excel-formel	Resultat
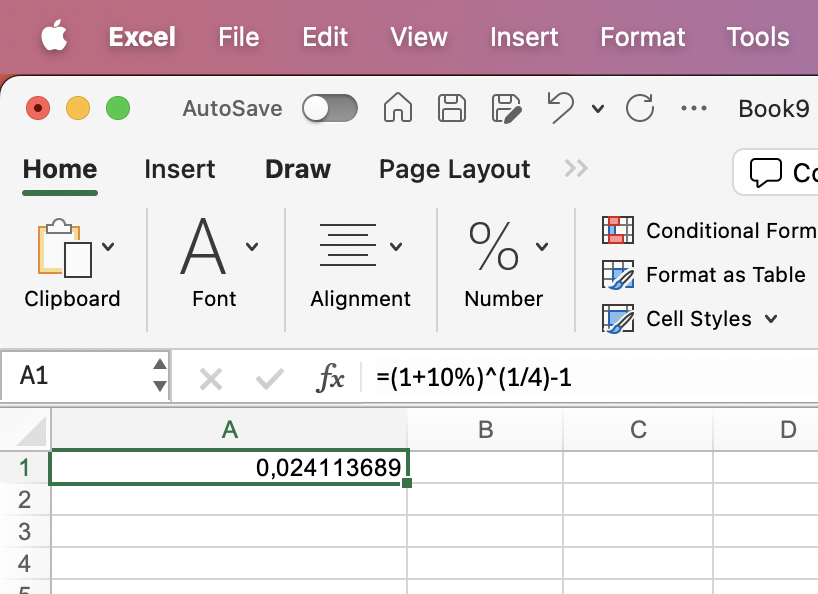
Hvad er den kvartalsvise rente, hvis den årlige effektive rente er 10%?	Årlig effektiv rente = 10% Terminer pr. år = 4	=(1+10%)^(1/4)-1	2,41%

Eksempel 3: Årlig til daglig rente

Tekst	Værdier	Excel-formel	Resultat
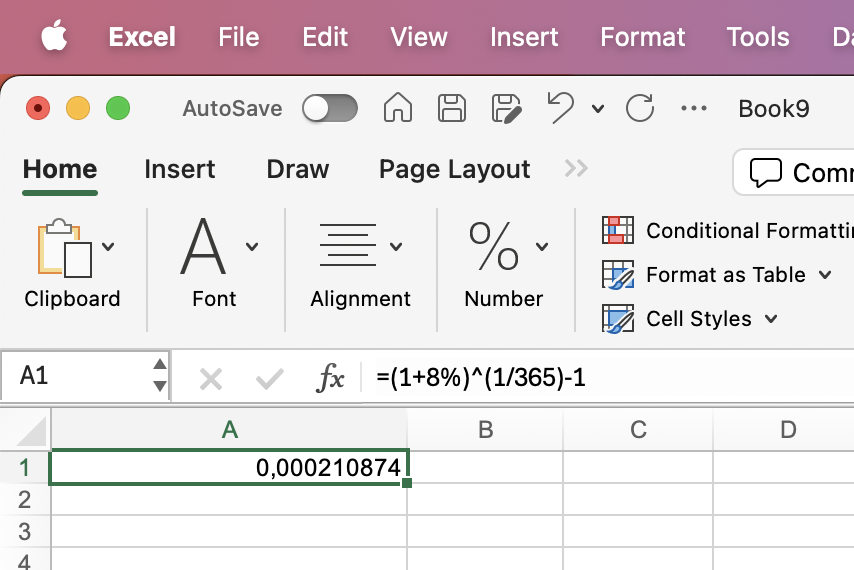
Hvad er den daglige rente, hvis den årlige effektive rente er 8%?	Årlig effektiv rente = 8% Terminer pr. år = 365	=(1+8%)^(1/365)-1	0,0211%

Disse eksempler illustrerer, hvordan man kan beregne terminsrenten ud fra den årlige effektive rente. Formlen er:
Terminsrente = (1 + årlig effektiv rente)^(1/antal terminer pr. år) - 1.
Bemærk, at terminsrenten altid vil være lavere end den årlige effektive rente divideret med antal terminer pr. år, på grund af renters rente effekten. Jo flere terminer pr. år, desto større bliver denne forskel.

Quiz